
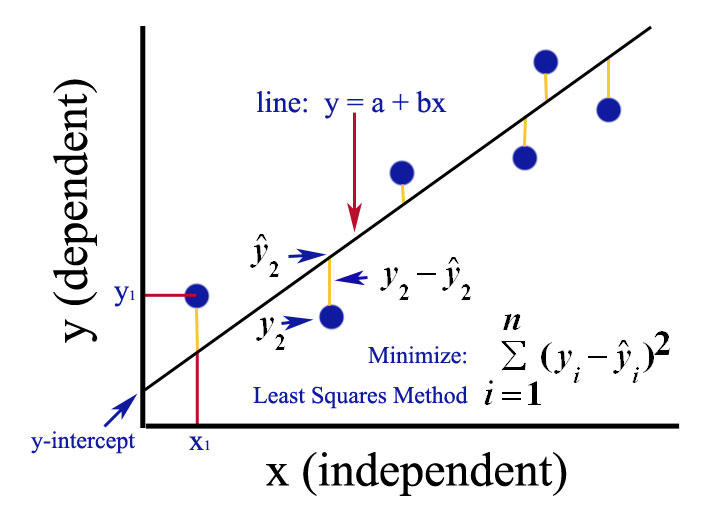
There are five rows of results, age, sex, education, language, and _cons (constant, which is the intercept in the formula above). The bottom table shows us the results from our regression analysis for each independent variable included. Reporting these are discipline specific and we will not go through these as they are not always used. These metrics are helpful in understanding the regression line in comparison to the data points. The second section of the output shows the calculated model fit measures such as SS (sum of squares) for the Model and the Residual (the amount of error in the model). We can see in this case the Adj R-squared value is the same as the R-sqaured, 0.297. The Adj R-squared accounts for this and adjusts for inflation from the number of variables included. Adj R-squared is important because the more independent variables we include in our model the higher our R squared value will become. This is a high value! Although, we need to look at the Adj R-squared that accounts for the number of independent variables in our model. A R-sqaured value of 0.297 is interpreted as the variables age, sex, education, and language explain 29.70% percent of the variance of individuals wages in this dataset. The next two lines labeled, R-sqaured and Adj R-squared, are used to judge our model fit. We can interpret this as our regression model is statistically significant and what we are examining ‘matters’. The significance is the statistical significance of the ANOVA test, which we can see is 0.0000, far below our.
T he F statistic (421.09) and degrees of freedom (4) are included in the second row with the significance (0.0000) reported below that. Next, we have the results from the ANOVA test that is used to test the statistical significance of the overall regression model indicating if our model is significant or not. Starting from the top row and moving down, we will go through each line of this section.įirst, we have 3,987 observations included in this analysis of listwise deletion. We find the model fit statistics to judge how well our independent variables explain the variance of wages. In the first output section to the right, Stata provides an overall summary of our regression model. We want to minimize this distance between our points and the regression line to have the best fit of our observed points. Lastly, $\epsilon$, is the error term of the regression formula, which is distance of each point ($i$ ) to the predicted regression line. The same goes for $sex(x_2)$, $education(x_3)$, and $language(x_4)$ which are the remaining independent variables, sex, education, and language, that are multiplied by the calculated coefficients in the model. Next, $age(x_1)$, is the variable age multiplied by the calculated regression coefficient that is added to $\beta_0$. We can think of $\beta_0$ as our starting wage value of the observations in the dataset. This is equal to $\beta_0$, the intercept of the model where our regression line intersects with the y axis when $x$ is zero. $_i$, is our dependent variable of the model that we are predicting with four independent variables of a specific observation $i$.

This is a continuous level variable measuring the number of years of education each respondent has. Education of respondent in years ( education).This is a nominal level variable measuring the sex of each respondent and is coded as 1= FEMALE and 2=MALE. This is a continuous level variable measuring the age of each respondent.
#MULTIPLE REGRESSION STATA CODE#
This is a continuous variable that ranges from a score of 2.30 to 49.92, which is a large range! If you would like to investigate this variable more use the code for the descriptive statistics to better understand the distribution, which is very important for a linear regression model. Below is a breakdown of the variables included in our model to help us keep track of the types of variables we are working with.


 0 kommentar(er)
0 kommentar(er)
